
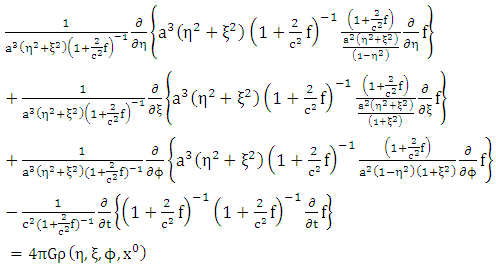
As a result, it contradicts the uncertainty principle for all the quantum states. The problem with the Einstein Field Equation is that it needs the momentum and the energy to be precise at every point of space-time. The latter also passed the experimental test, but unlike the further, it doesn’t have specifications. Even though the theory and the set of equations have passed the rest, they are incompatible with the known quantum theory.
The Einstein Field Equation is not accurate. How Accurate is the Einstein Field Equation of Gravity? The trajectories of these particles can then be found by the geodesic equations. The solutions of these equations are the components of the metric tensor that specifies the space-time geometry. It is also equated with momentum and energy at that point. It is determined by the curvature of time and space at a particular point of time and space. It describes gravity as a result of the space-time that is curved by both mass and energy. Initially published in 1915, it is also widely called a tensor equation in the field of physics. It is actually the combination of ten different equations that are contained in the tensor equation. Einstein’s equation describes the interaction of gravitation. It is a set of ten equations that are extracted from the General Theory of Relativity, by Albert Einstein. But really unless you are in a production environment the time spent on further analysis is not really cost effective given how fast this executes as it is.The Einstein Field Equation is also known as Einstein’s equation. It is quite obvious that the desired root is close to $x=170$, so starting with $0$ as the left hand limit for the bisection can be improved. The solution method can be improved somewhat if you send some time analysing the problem. If ff(a,Nknots)*y > tic,MyMain(100,1e-12),tocĬhanging from n=100 to n=10000 in Simpson's rule less than doubles the computational time required. So if I understand this correctly, we need to use Simpson's rule to evaluate $x_l$ where
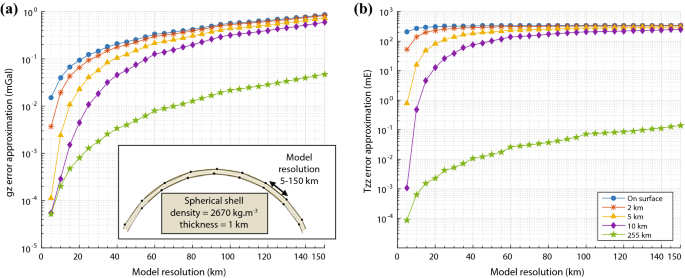
When $R=200$ and $L=170.$ Evaluate all the integrals by using the composite Simpson's rule. Use Matlab and numerical methods to find $x_l$ so that


 0 kommentar(er)
0 kommentar(er)
